Analytical solutions for two-phase

Laplace’s law

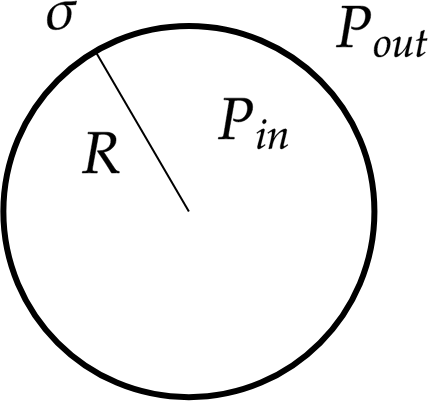
The difference between the pressure inside the droplet \(P_{in}\) and the pressure outside \(P_{out}\) is equal to

(324)\[\underbrace{P_{in}-P_{out}}_{\Delta P}=\frac{\sigma}{R}\]

where \(\sigma\) is the surface tension and \(R\) is the droplet radius.

Analytical solution of double-Poiseuille flow

(325)\[\begin{split}u_{x}(y)=\begin{cases} \frac{Gh^{2}}{2\eta_{A}}\left[-\left(\frac{y}{h}\right)^{2}-\frac{y}{h}\left(\frac{\eta_{A}-\eta_{B}}{\eta_{A}+\eta_{B}}\right)+\frac{2\eta_{A}}{\eta_{A}+\eta_{B}}\right] & \mbox{if }0\leq y\leq h\\ \frac{Gh^{2}}{2\eta_{B}}\left[-\left(\frac{y}{h}\right)^{2}-\frac{y}{h}\left(\frac{\eta_{A}-\eta_{B}}{\eta_{A}+\eta_{B}}\right)+\frac{2\eta_{B}}{\eta_{A}+\eta_{B}}\right] & \mbox{if }-h\leq y\leq0 \end{cases}\end{split}\]

Analytical solution of Prosperetti for capillary wave

The example of such a study is given by the test case of capillary wave. For that test case, an analytical solution exists [2]_. The objective is to study the influence of mesh on the solution accuracy. The amplitude is

(326)\[a(t)=\frac{4(1-4\beta)\nu^{2}k^{4}}{8(1-4\beta)\nu^{2}k^{4}+\omega_{0}^{2}}a_{0}\text{erfc}(\nu k^{2}t)^{1/2}+\sum_{i=1}^{4}\frac{z_{i}}{Z_{i}}\left(\frac{\omega_{0}^{2}a_{0}}{z_{i}^{2}-\nu k^{2}}-u_{0}\right)\times\exp[(z_{i}^{2}-\nu k^{2})t]\text{erfc}(z_{i}t^{1/2})\]

where \(\nu\) is the kinematic viscosity which is identical for both fluids, \(k\) is the wave number which is related to the wavelength \(\lambda\) by \(k=2\pi/\lambda\). The coefficient \(\beta\) is defined by the liquid \(\rho_l\) and gas \(\rho_g\) densities:

(327)\[\beta=\frac{\rho_{l}\rho_{g}}{(\rho_{l}+\rho_{g})^{2}}\]

\(\omega_0\) is the inviscid natural frequency given by

(328)\[\omega_{0}=\frac{\rho_{l}-\rho_{g}}{\rho_{l}+\rho_{g}}gk+\frac{\sigma k^{3}}{\rho_{l}+\rho_{g}}\]

where \(g\) is the gravity. In the following verifications \(g=0\). The \(z_i\)’s are the four roots of the algebric equation

(329)\[z^{4}-4\beta(k^{2}\nu)^{1/2}z^{3}+2(1-6\beta)k^{2}\nu z^{2}+4(1-3\beta)(k^{2}\nu)^{3/2}z+(1-4\beta)\nu^{2}k^{4}+\omega_{0}^{2}=0\]

and

(330)\[Z_{1}=(z_{2}-z_{1})(z_{3}-z_{1})(z_{4}-z_{1})\]