Local and instantaneous Navier-Stokes equations
Two-fluid formulation without phase-change
That section is a summary of [1] (section 3.2 page 205). We consider a control volume Fig. 39 with two fluids of index 1 and 2 seprated by one interface. The volume of each fluid is \(V_k\) with \(k=1,2\), the surrounding surface is noted \(A_k\) and the surface of separation is \(A_i\) where the index \(i\) means interface.
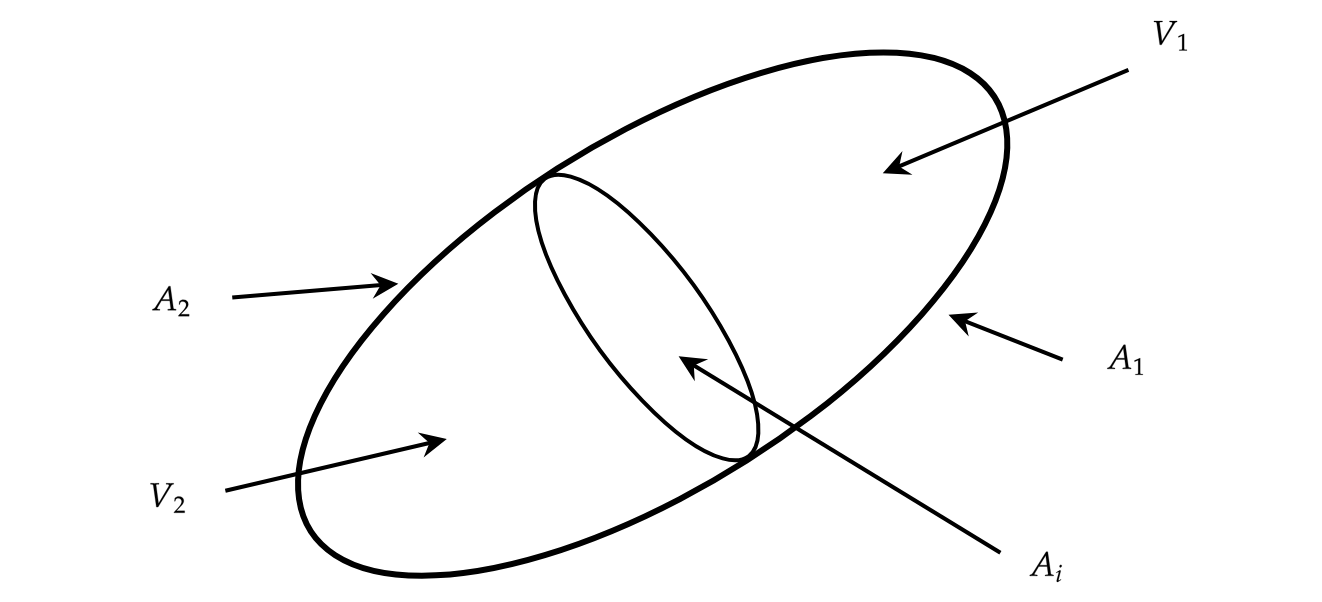
Fig. 39 Control volume of two-phase flows
Mass balance
The mass balance for each fluid writes
In more compact form with index \(k=1,2\) for fluid 1 and fluid 2:
The local and instantaneous equation at interface writes:
It expresses the mass balance through the interface. It is common to set:
where \(\dot{m}_{k}\) is the local mass flux of phase \(k\) which goes out the domain occupied by phase \(k\) at one point of the interface. With that quantity Eq. (314) writes:
If we assume that both fluids do not slip, then the tangential velocities are identical \(\boldsymbol{u}_{1}^{t}=\boldsymbol{u}_{2}^{t}\) and
Without phase change and no-slip of both fluids, the velocity of each phase is identical.
Impulsion balance with surface tension
The impulsion balance for each bulk phase writes:
where \(\overline{\overline{\boldsymbol{T}}}_{k}\) is the stress tensor which is defined by Eq. (267) for each phase \(k\). At interface, the impulsion balance through an element of interface writes
where \(\sigma\) is the surface tension and \(\boldsymbol{n}_{i}\) is the unit normal vector of \(C\) and directed toward outside the volume \(V\). The impulsion balance the local instantaneous relation at interface:
where \(s\) is the curvilinear coordinate at interface, \(\boldsymbol{t}\) is the tangential unit vector at interface and \(R\) is the curvature radius. The term \(d\sigma/ds\) is related to Marangoni effects due to variation of surface tension with temperature or concentration at interface. The term \(\sigma\boldsymbol{n}_{1}/R\) is the Young-Laplace term. In static case, we obtain:
One-fluid formulation for incompressible fluids
In one-fluid formulation, there are only one mean velocity \(\boldsymbol{u}\) and one mean pressure for two fluids of bulk densities \(\rho_1\) and \(\rho_2\) and dynamic viscosity \(\eta_1\) and \(\eta_2\). We must introduce a new numerical quantity to track the interface and respect the jump conditions.